Tan^2 identities 265537-Tan 2 identities

Using double angle identities in trigonometry Identities in math shows us equations that are always true There are many trigonometric identities (Download the Trigonometry identities chart here ), but today we will be focusing on double angle identities, which are named due to the fact that they involve trig functions of double angles such as sin θ \theta θ, cos2 θ \theta θ, and tan2The sum identity for tangent is derived as follows To determine the difference identity for tangent, use the fact that tan (−β) = −tanβ Example 1 Find the exact value of tan 75° Because 75° = 45° 30° Example 2 Verify that tan (180° − x) = −tan x Example 3 Verify that tan (180° x) = tan x Example 4 Verify that tan (360° − x) = − tan xIf tan ⁡ 2 θ = m n, \tan^2\theta=\frac { m }{ n }, tan 2 θ = n m , where m m m and n n n are coprime positive integers, find m n mn m n

Double Angle Formulas Trigonometry Teachoo 2x 3x Formula Provi

Tan 2 identities

Tan 2 identities-2 The Elementary Identities Let (x;y) be the point on the unit circle centered at (0;0) that determines the angletrad Recall that the de nitions of the trigonometric functions for this angle are sint = y tant = y x sect = 1 y cost = x cott = x y csct = 1 x These de nitions readily establish the rst of the elementary or fundamental identities given in the table belowFirst using trigonometric identities One of the most common is the Pythagorean identity, 2 2 sin ( ) cos ( ) 1 which allows you to rewrite )2 sin ( in terms of )2 cos ( or vice versa, 22 22 sin ( ) 1 cos ( ) cos ( ) 1 sin ( ) This identity becomes very useful whenever an equation involves a

Summary Of Trigonometric Identities

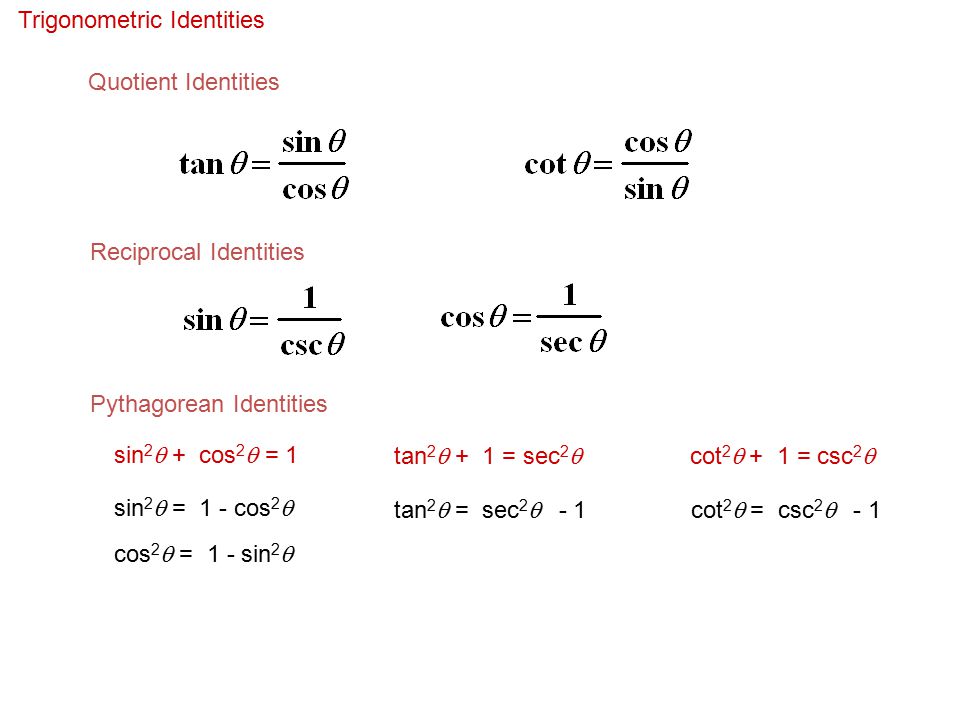
The list of these identities is as follows 1) csc θ = 1/sin θ 2) sin θ= 1/csc θ 3) sec θ = 1/cos θ 4) cos θ = 1/sec θ 5) cot θ = 1/tan θ 6) tan θ= 1/cot θ 7) tan θ = sin θ/cos θ 8) cot θ = cos θ/sin θ1tan 2 θ = sec 2 θ;2 2 2 sin22sincos cos2cossin 2cos1 12sin 2tan tan2 1tan qqq qqq q q q q q = ====Degrees to Radians Formulas If x is an angle in degrees and t is an angle in radians then 180 and txt tx x pp p =Þ== Half Angle Formulas (alternate form) (( )) (( )) ( ) ( ) 2 2 2 1cos1 sinsin1cos2 222 1cos1 coscos1cos2 222 1cos 1cos2 tantan 21cos1cos2

The Pythagorean Identities are based on the properties of a right triangle cos2θ sin2θ = 1 1 cot2θ = csc2θ 1 tan2θ = sec2θ The evenodd identities relate the value of a trigonometric function at a given angle to the value of the function at the opposite angle tan(− θ)The key Pythagorean Trigonometric identity are sin 2 (t) cos 2 (t) = 1 tan 2 (t) 1 = sec 2 (t) 1 cot 2 (t) = csc 2 (t) So, from this recipe, we can infer the equations for different capacities additionally Learn more about Pythagoras Trig IdentitiesIf tan 2, then 4 If csc a, then 5 If sec 1, then cos 1 6 If cot 1, then tan 1 Ratio Identities Unlike the reciprocal identities, the ratio identities do not have any common equivalent forms Here is how we derive the ratio identity for tan sin cos y r x r y x tan sin 1 a cot 1 2 sec 2 √3 cos √3 2 csc 1 sin 1 3 5 5 3 csc 5 3 sin

Cos2θ = 1 cos2θ 2 sin2θ = 1 − cos2θ 2 Knowing the half angle identities in the above form will be the most useful for applications in calculus That said, why these identities are called the "half angle" identities is made more clear upon making a substitution of x = 2θ and then taking a square root cos(x 2) = √1 cosx 2 sin(xFree multiple angle identities list multiple angle identities by request stepbystep This website uses cookies to ensure you get the best experience multipleangleidentitiescalculator identity \tan(2x) en Related Symbolab blog posts High School Math Solutions – Trigonometry Calculator, Trig IdentitiesAsk for it or check my other videos and playlists!##### PLAYLISTS #####

Double Angle And Multiple Angle Identities

Trigonometric Identities A Plus Topper

 You can check some important questions on trigonometry and trigonometry all formula from below 1 Find cos X and tan X if sin X = 2/3 2 In a given triangle LMN, with a right angle at M, LN MN = 30 cm and LM = 8 cm Calculate the values of sin L, cos L, and tan L 3Following table gives the double angle identities which can be used while solving the equations You can also have sin2θ,cos2θ expressed in terms of tanθ as under sin2θ = 2tanθ 1 tan2θ cos2θ = 1 −tan2θ 1 tan2θSin (x y) = sin x cos y cos x sin y cos (x y) = cos x cosy sin x sin y tan (x y) = (tan x tan y) / (1 tan x tan y) sin (2x) = 2 sin x cos x cos (2x) = cos ^2 (x) sin ^2 (x) = 2 cos ^2 (x) 1 = 1 2 sin ^2 (x) tan (2x) = 2 tan (x) / (1 tan ^2 (x)) sin ^2 (x) = 1/2 1/2 cos (2x) cos ^2 (x) = 1/2 1/2 cos (2x) sin x sin y = 2 sin ( (x y)/2 ) cos ( (x y)/2 )

Trigonometric Identities

Summary Of Trigonometric Identities

Tan (x) is an odd function which is symmetric about its origin tan (2x) is a doubleangle trigonometric identity which takes the form of the ratio of sin (2x) to cos (2x) sin (2x) = 2 sin (x) cos (x) cos (2x) = (cos (x))^2 – (sin (x))^2 = 1 – 2 (sin (x))^2 = 2 (cos (x))^2 – 1 Proof 71K views · View upvotes ·Create an identity for the expression \(2 \tan \theta \sec \theta\) by rewriting strictly in terms of sine Solution There are a number of ways to begin, but here we will use the quotient and reciprocal identities to rewrite the expressionLet's start with the left side since it has more going on Using basic trig identities, we know tan (θ) can be converted to sin (θ)/ cos (θ), which makes everything sines and cosines 1 − c o s ( 2 θ) = ( s i n ( θ) c o s ( θ) ) s i n ( 2 θ) Distribute the right side of the equation 1 − c o s ( 2 θ) = 2 s i n 2 ( θ)

S A T C Trigonometry Applying Astc Reference Coterminal Angles Ppt Video Online Download

Important Trigonometric Identiti

Periodicity of trig functions Sine, cosine, secant, and cosecant have period 2 π while tangent and cotangent have period π Identities for negative angles Sine, tangent, cotangent, and cosecant are odd functions while cosine and secant are even functions Ptolemy's identities, the sum and difference formulas for sine and cosine$\tan^2{\theta} \,=\, \sec^2{\theta}1$ The square of tan function equals to the subtraction of one from the square of secant function is called the tan squared formula It is also called as the square of tan function identity Introduction The tangent functions are often involved in trigonometric expressions and equations in square form The expressions or equations can be possibly simplified by transforming the tanTRIGONOMETRIC IDENTITIES By Joanna GuttLehr, Pinnacle Learning Lab, last updated 5/08 Pythagorean Identities sin (A) cos (A) 1 1 tan (A) sec (A) 1 cot (A) csc2 (A)Quotient Identities sin( )

Cofunction Identities In Trigonometry With Proof And Examples Owlcation

Http Tutorial Math Lamar Edu Pdf Trig Cheat Sheet Reduced Pdf

Tan(x y) = (tan x tan y) / (1 tan x tan y) sin(2x) = 2 sin x cos x cos(2x) = cos 2 (x) sin 2 (x) = 2 cos 2 (x) 1 = 1 2 sin 2 (x) tan(2x) = 2 tan(x) / (1 The Pythagorean identities are based on the properties of a right triangle cos2θ sin2θ = 1 1 cot2θ = csc2θ 1 tan2θ = sec2θ The evenodd identities relate the value of a trigonometric function at a given angle to the value of the function at the opposite angle tan( − θ) = − tanθ cot( − θ) = − cotθTan x/2 = (sin x/2)/ (cos x/2) (quotient identity) tan x/2 = ±√ (1 cos x)/ 2 / ±√ (1 cos x)/ 2 (halfangle identity) tan x/2 = ±√ (1 cos x)/ (1 cos x) (algebra) Halfangle identity for tangent • There are easier equations to the halfangle identity for tangent equation tan x/2 = sin x/ (1 cos x) 1st easy equation

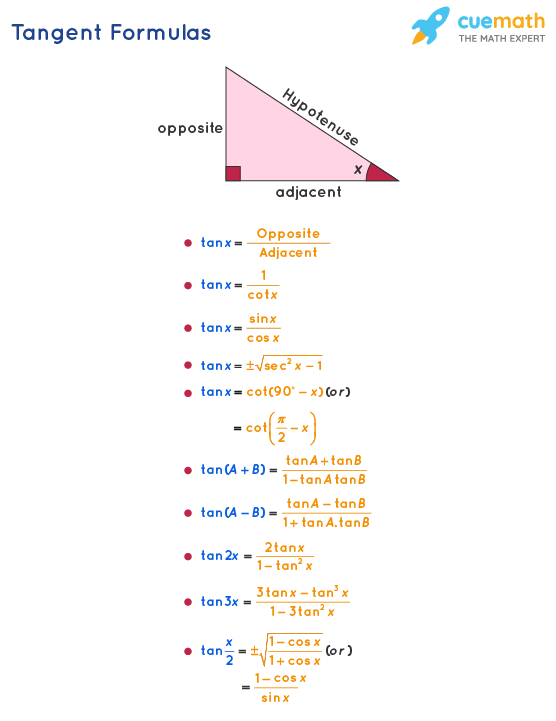
Tangent Formula What Are Tangent Formulas Examples

Summary Of Trigonometric Identities

Now, using the trigonometric identity 1tan 2 a = sec 2 a sec 2 A = 1 (3/4) 2 sec 2 A = 25/16 sec A = ±5/4 Since, the ratio of lengths is positive, we can neglect sec A = 5/4 Therefore, sec A = 5/4 Example 2 (1 – sin A)/(1 sin A) = (sec A – tan A) 2 Solution Let us take the Left hand side of the equation LHS = (1 – sin A)/(1 sin A)Sec 2 t = 1 tan 2 t Identities expressing trig functions in terms of their supplements sin( – t) = sin t cos( – t) = –cos t tan( – t) = tan t Difference formulas for sine and cosine sin (s – t) = sin s cos t – cos s sin t cos (s – t) = cos s cos t sin s sin t Sum, difference, andWhat Are Trigonometric Identites used for?

Double Angle Formulas Trigonometry Teachoo 2x 3x Formula Provi

Art Of Problem Solving

Didn't find what you were looking for?Tan2x Formula = 2 tan x 1 − t a n 2 x Now, we need to recall the addition formula, t a n ( a b) = tan a tan b 1 − tan a tan b So, for the double angle formula, here let the values of both the angles be a (a = b) t a n ( a a) = tan a tan a 1 − tan a tan a Tan 2a = 2 tan a 1 − t a n 2 aTan( )= tan tan 1−tan tan tan( − )= tan −tan 1tan tan Double–Angle Identities sin 2𝜃=2 sin𝜃 cos𝜃 cos 2 𝜃 = cos 2𝜃−sin2𝜃 =2 cos2θ−1 =1−2 sin2𝜃 tan 2𝜃= 2 tan𝜃 1−tan2𝜃

Tangent Half Angle Formula Wikipedia Republished Wiki 2

1

(x 5)(x − 5) = x 2 − 25 The significance of an identity is that, in calculation, we may replace either member with the other We use an identity to give an expression a more convenient form In calculus and all its applications, the trigonometric identities are of central importance On this page we will present the main identitiesThese identities are known collectively as the tangent halfangle formulae because of the definition of These identities can be useful in calculus for converting rational functions in sine and cosine to functions of t in order to find their antiderivatives1 tan 2 ( x ) = sec 2 ( x ) 1 cot 2 ( x ) = csc 2 ( x ) There are also the reciprocal identities

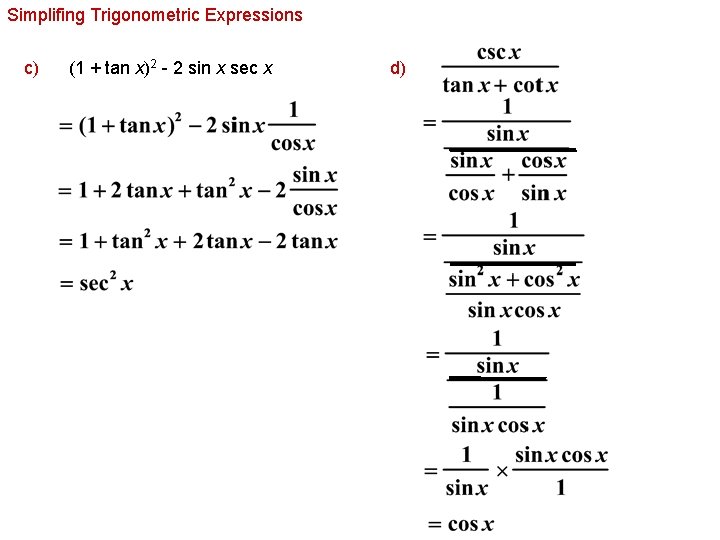
While You Wait Trigonometric Identities And Equations Section

Powers Of Trigonometric Functions

List of trigonometric identities 2 Trigonometric functions The primary trigonometric functions are the sine and cosine of an angle These are sometimes abbreviated sin(θ) andcos(θ), respectively, where θ is the angle, but the parentheses around the angle are often omitted, eg, sin θ andcos θ The tangent (tan) of an angle is the ratio of the sine to the cosineReciprocal identities sinu= 1 cscu cosu= 1 secu tanu= 1 cotu cotu= 1 tanu cscu= 1 sinu secu= 1 cosu Pythagorean Identities sin 2ucos u= 1 1tan2 u= sec2 u 1cot2 u= csc2 u Quotient Identities tanu= sinu cosu cotu= cosu sinu CoFunction Identities sin(ˇ 2 u) = cosu cos(ˇ 2 u) = sinu tan(ˇ 2 u) = cotu cot(ˇ 2 u) = tanu csc(ˇ 2 u) = secu sec Which of the following is a trigonometric identity?

5 2 Verifying Trigonometric Identities Copyright Cengage Learning

Trig Identities Bingo Card

The trigonometric identities are used for solving various geometric, trigonometric, and other math problems They are equations that are always true How to Prove Trigonometric Identies?There are three basic trigonometric identities in class 10 which relate the trigonometric ratios mutually The three basic trigonometric identities learned in class 10 are Sin 2 A Cos 2 A = 1 Sec 2 A = 1 Tan 2 A Cosec 2 A = 1 Cot 2 A These identities can be derived by considering the right triangle The right triangle is subjected toTrigonometric cofunction identities are relationships between the basic trigonometric functions (sine and cosine) based on complementary anglesThey also show that the graphs of sine and cosine are identical, but shifted by a constant of π 2 \frac{\pi}{2} 2 π The identities are extremely useful when dealing with sums of trigonometric functions, as they often allow for use of the

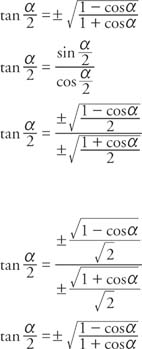
Tangent Identities

3

 Simplify tan^2 x sec^2 Ans 1 Use trig identity 1 tan^2 x = sec^2 x tan^2 x sec^2 x = 1 1tan^2x=sec^2x Change to sines and cosines then simplify 1tan^2x=1(sin^2x)/cos^2x =(cos^2xsin^2x)/cos^2x but cos^2xsin^2x=1 we have1tan^2x=1/cos^2x=sec^2x Trigonometry ScienceA cot θ tan θ = 1b sec^2 θ csc^2 θ = 1c tan^2 θ = sin^2 θ x sec^2 θ d cos^2 θ = sec^2 θ x tan^2 θ

How To Use Double Angle Identities Studypug

Double Angle And Multiple Angle Identities

The three trigonometric identities are sin 2 θ cos 2 θ = 1;Trigonometric Identities Pythagorean Identities cos 2 θ sin 2 θ = 1 1 tan 2 θ = sec 2 θ 1 cot 2 θ = csc 2 θ cos 2 θ sin 2 θ = 1 1 tan 2 θ = sec 2 θ 1 cot 2 θ = csc 2 θ EvenOdd Identities cos (− θ) = cos θ sec (− θ) = sec θ sin (− θ) = − sin θ tan (− θ) = − tan1cot 2 θ = cosec 2 θ;

A Trig Identity

Solved Trig Identities 1 Sin Cos 2 Sin Cos 2 2 2 Tan2 Cos2 Cot2 Sin2 1 3 Sec Course Hero

In this video I go over the proof of the trigonometry identity tan^2(x) 1 = sec^2(x) The proof of this identity is very simple and like many other trig idTrigonometricidentityprovingcalculator prove \tan^2(x)\sin^2(x)=\tan^2(x)\sin^2(x) en

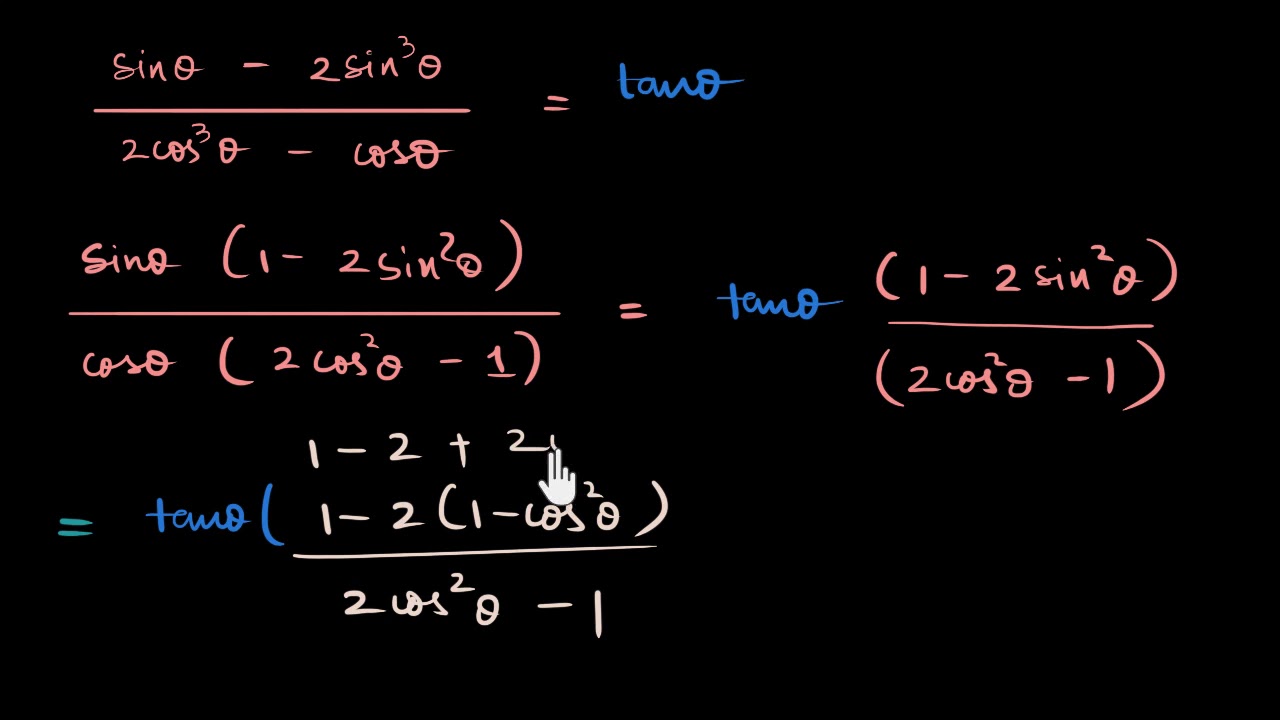
Trigonometric Identity Example Proof Involving Sin Cos And Tan Video Khan Academy

11 Basic Trigonometric Identities An Identity Is An Equation That Is True For All Defined Values Of A Variable We Are Going To Use The Identities To Ppt Download

14 2 Trigonometric Identities

Verify The Identity Tan X Cot X 2 Sec2 X Chegg Com

Trigonometric Identities List Of Trigonometric Identities Examples

Ilectureonline

Get Answer Prove The Given Identity Cos 2 Theta 1 Tan2 Theta 1 Which Transtutors

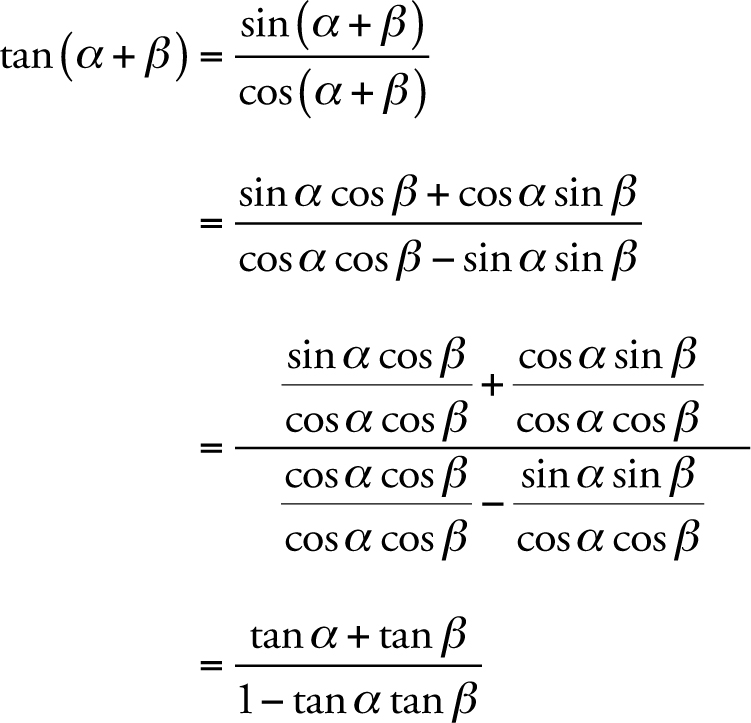
Tangent Identities

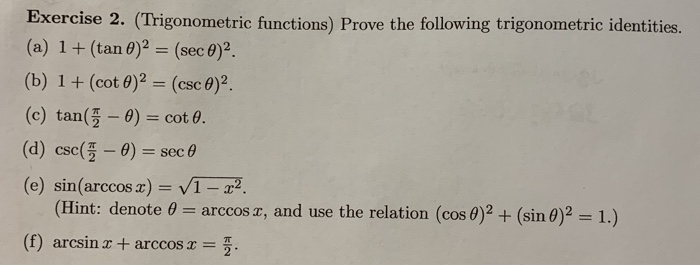
Exercise 2 Trigonometric Functions Prove The Chegg Com

List Of Trigonometric Identities Wikipedia

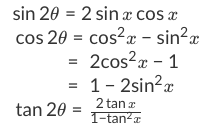
How To Use Double Angle Identities Studypug

Lt 14 I Know The Trig Identities Blaine High School Precalculus

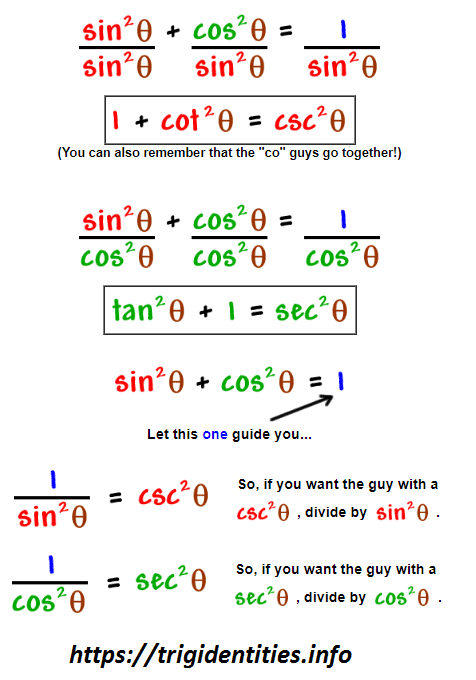
Pythagorean Trig Identities Recall Pythagoras Theorem Trig Identities

2 Prove The Following Trig Identities A Prove Tan Chegg Com

Ppt Analytic Trig Powerpoint Presentation Free Download Id

Trigonometric Identities Simplify Expressions Video Lessons Examples And Solutions

Integrate Tan 2x

Integrate Sec 2x Method 2

Tangent Half Angle Formula Wikipedia

6 2 Verifying Trigonometric Identities

Trigonometric Functions Of Double Angles Double Angle Formulas Trigonometric Functions Expressed By The Half Angle Trigonometric Identities Examples

1

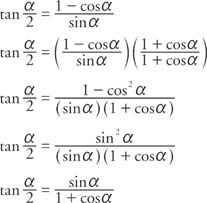
Tangent Identities

Precalculus Trigonometry Trig Identities 29 Of 57 Formula For Lowering Power Tan 2 X Youtube

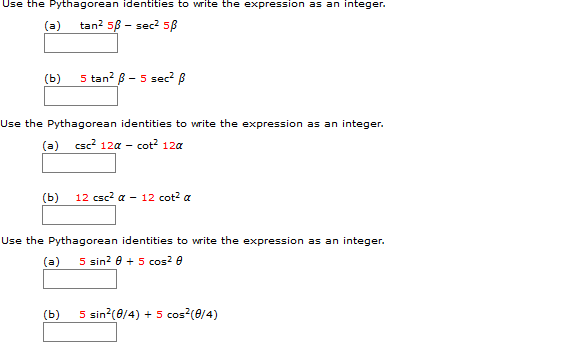
Use The Pythagorean Identities To Write The Chegg Com

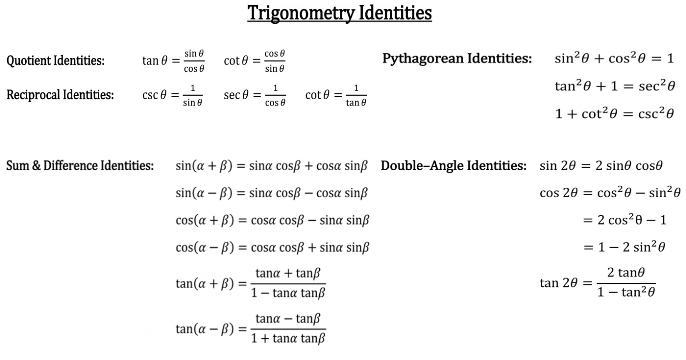
How To Prove Quotient And Reciprocal Identities Studypug

Important Trigonometric Identiti

Trigonometric Identity 1 Sin X 1 Sin X Sec X Tan X 2 Cbse 10 Youtube

How Do You Verify The Identity Tan2theta 2 Cottheta Tantheta Socratic

Http Tutorial Math Lamar Edu Pdf Trig Cheat Sheet Pdf

Trigonometric Identities Topics In Trigonometry

Proof Tan 2 1 Sec 2 Youtube

10 Identity Tan Squared X 1 Sec Squared X Trigonometry Educator Com

Integrate Sec 2x Method 1

What Are The Quotient Identities For A Trigonometric Functions Socratic

Www Brockport Edu Academics Tutoring Docs Trigonometric Identities Pdf

Tangent Half Angle Formula Wikipedia

3

Every Day I M Calculatin I D3 Unit Q Pythagorean Identities

Www2 Math Binghamton Edu Lib Exe Fetch Php People Mckenzie Trig Identities Worksheet With Answers 2 Pdf

Ppt Warm Up Powerpoint Presentation Free Download Id

Tangent Identities

Summary Of Trigonometric Identities

Sites Math Washington Edu Putnam Handouttrig Pdf

Cofunction And Reduction Identities

Summary Of Trigonometric Identities

How Do You Use Double Angle Identities To Solve Equations Socratic

Establish The Identity 1 Tan 2 Theta 1 Tan 2 Chegg Com

How I Remember Trig Identities Part 2 Beyond Solutions

5 1 Fundamental Trig Identities Reciprocal Identities Sin

5 1 5 2 Trigonometric Identities Ppt Download

Pythagorean Trig Identities Recall Pythagoras Theorem Trig Identities

Tangent Half Angle Formula Wikipedia

Verify The Identity Tan 2 0 1 Cos 2 1 Tan 2 Chegg Com

Trigonometric Identities A Plus Topper

1 Tan 2x 1 Tan 2 X 1 2cos 2 X Youtube

What Is The Formula Of Tan2x Quora

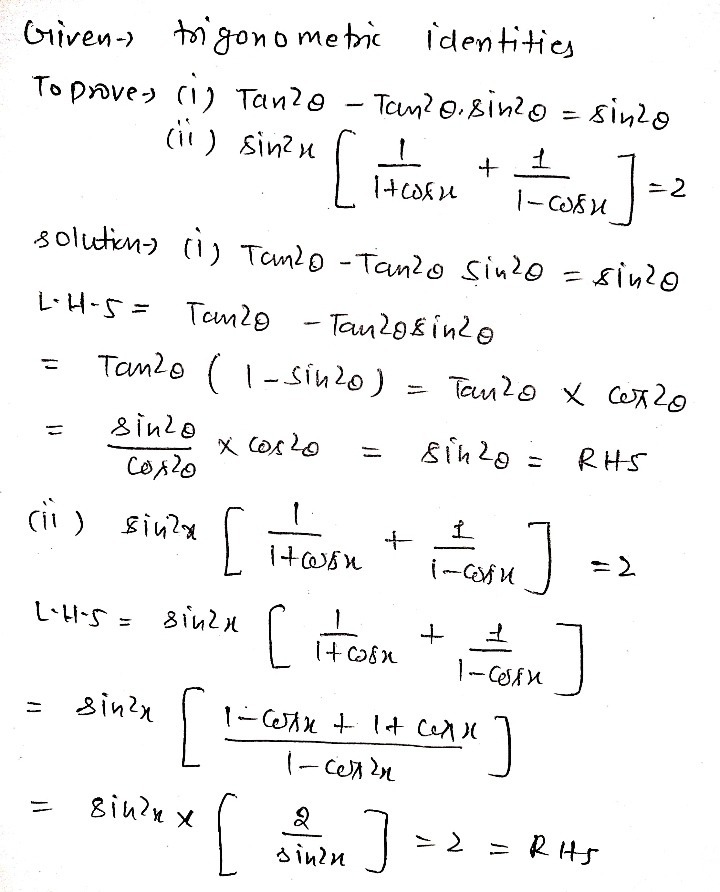
Prove The Following Identities Tan 2 8 Tan 2 Gauthmath

Trig Identities And Formulas Pre Calculus Quiz Quizizz

Cos Sin Tan Csc Sec Cot

Trigonometry Identity Tan 2 X 1 Sec 2 X Youtube

Trigonometric Identities A Plus Topper

Half Angle Or Double Angle Examples Examples Solutions Videos Worksheets Games Activities

How Do You Prove The Identities Cosx Secx Sinx Cscx Sec 2x Tan 2x Socratic

Tangent Identities

Warm Up Prove Sin 2 X Cos 2 X 1 This Is One Of 3 Pythagorean Identities That We Will Be Using In Ch 11 The Other 2 Are 1 Tan 2 X Sec 2 X Ppt Download

Pinkmonkey Com Trigonometry Study Guide 4 4 Tangent Identities

13 1 Trigonometric Identities Ppt Video Online Download

Trigonometric Identities

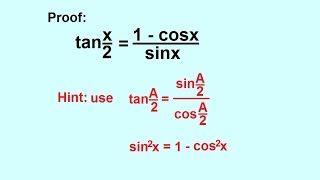
Precalculus Trigonometry Trig Identities 34 Of 57 Proof Half Angle Formula Tan X 2 Youtube

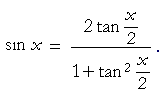
Trigonometric Identities Topics In Trigonometry

Summary Of Trigonometric Identities

Sin Cos Cos 2 Sin 2 Tan 1 Tan 2 Youtube

Addition And Subtraction Formulas For Tangent And Cotangent

Derivatives Of Trigonometric Functions

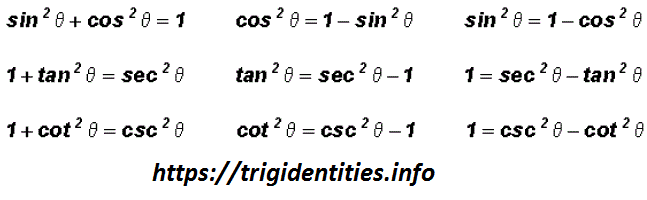
Pythagorean Trig Identities Recall Pythagoras Theorem Trig Identities

How Do You Simplify 1 Tan 2 X 1 Tan 2 X Socratic

How Do You Prove The Identity Tan 2x Secx 1 1 Cosx Cosx Socratic

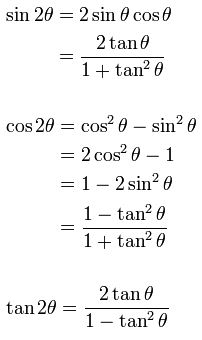
Trigonometric Identities Definition Rules Examples S Sigma Tricks

How Do You Simplify Sec 4x Tan 4x Sec 2x Tan 2x Socratic

Incoming Term: tan 2 identities, tan 2 theta identities, tan 2 x identities, identities of tan 2,